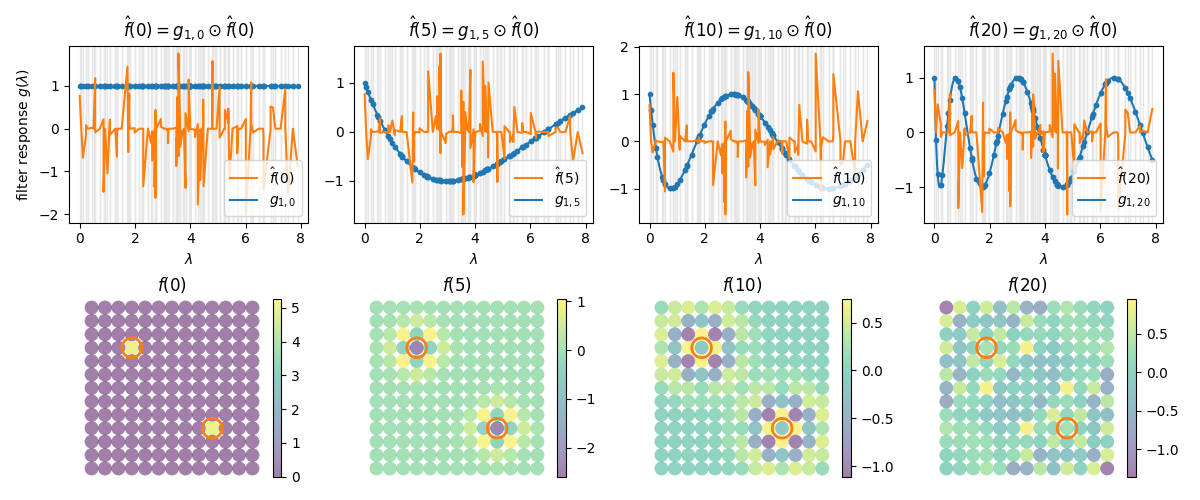
Wave propagation

Solve the wave equation by filtering the initial conditions with the wave kernel pygsp.filters.Wave.

from os import path

import numpy as np
from matplotlib import pyplot as plt
import pygsp as pg

n_side = 13
G = pg.graphs.Grid2d(n_side)
G.compute_fourier_basis()

sources = [
    (n_side//4 * n_side) + (n_side//4),
    (n_side*3//4 * n_side) + (n_side*3//4),
]
x = np.zeros(G.n_vertices)
x[sources] = 5

times = [0, 5, 10, 20]

fig, axes = plt.subplots(2, len(times), figsize=(12, 5))
for i, t in enumerate(times):
    g = pg.filters.Wave(G, time=t, speed=1)
    title = r'$\hat{{f}}({0}) = g_{{1,{0}}} \odot \hat{{f}}(0)$'.format(t)
    g.plot(alpha=1, ax=axes[0, i], title=title)
    axes[0, i].set_xlabel(r'$\lambda$')
#    axes[0, i].set_ylabel(r'$g(\lambda)$')
    if i > 0:
        axes[0, i].set_ylabel('')
    y = g.filter(x)
    line, = axes[0, i].plot(G.e, G.gft(y))
    labels = [r'$\hat{{f}}({})$'.format(t), r'$g_{{1,{}}}$'.format(t)]
    axes[0, i].legend([line, axes[0, i].lines[-3]], labels, loc='lower right')
    G.plot(y, edges=False, highlight=sources, ax=axes[1, i], title=r'$f({})$'.format(t))
    axes[1, i].set_aspect('equal', 'box')
    axes[1, i].set_axis_off()

fig.tight_layout()

Estimated memory usage: 9 MB