Random walks

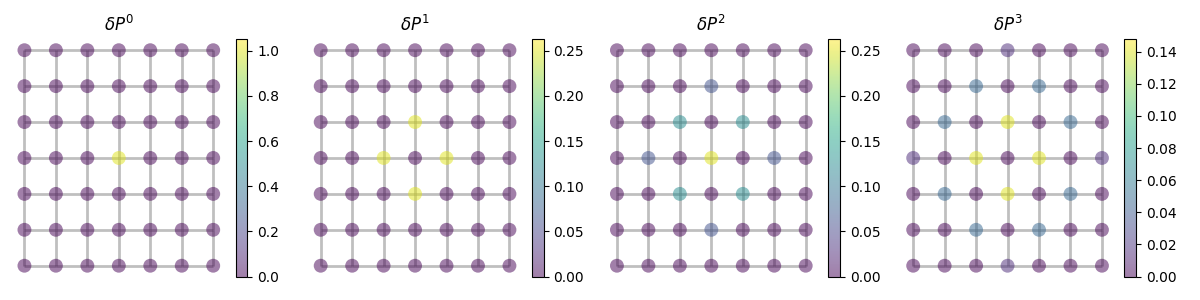
Probability of a random walker to be on any given vertex after a given number of steps starting from a given distribution.

# sphinx_gallery_thumbnail_number = 2

import numpy as np
from scipy import sparse
from matplotlib import pyplot as plt
import pygsp as pg

N = 7
steps = [0, 1, 2, 3]

graph = pg.graphs.Grid2d(N)
delta = np.zeros(graph.N)
delta[N//2*N + N//2] = 1

probability = sparse.diags(graph.dw**(-1)).dot(graph.W)

fig, axes = plt.subplots(1, len(steps), figsize=(12, 3))
for step, ax in zip(steps, axes):
    state = (probability**step).__rmatmul__(delta)  ## = delta @ probability**step
    graph.plot(state, ax=ax, title=r'$\delta P^{}$'.format(step))
    ax.set_axis_off()

fig.tight_layout()

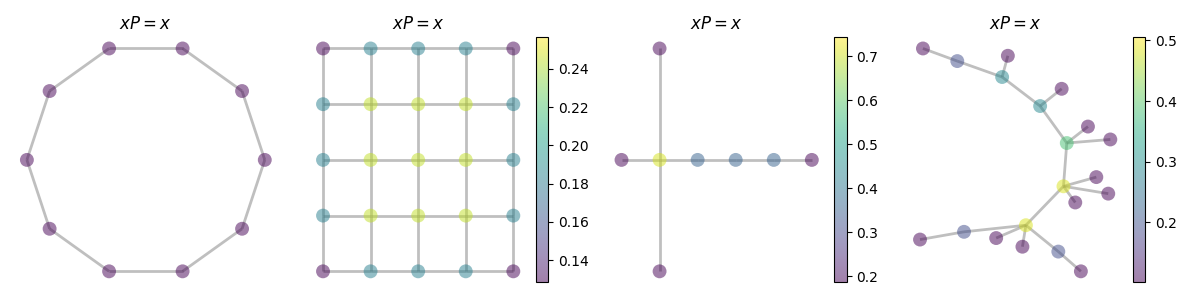
Stationary distribution.

graphs = [
    pg.graphs.Ring(10),
    pg.graphs.Grid2d(5),
    pg.graphs.Comet(8, 4),
    pg.graphs.BarabasiAlbert(20, seed=42),
]

fig, axes = plt.subplots(1, len(graphs), figsize=(12, 3))

for graph, ax in zip(graphs, axes):

    if not hasattr(graph, 'coords'):
        graph.set_coordinates(seed=10)

    P = sparse.diags(graph.dw**(-1)).dot(graph.W)

#    e, u = np.linalg.eig(P.T.toarray())
#    np.testing.assert_allclose(np.linalg.inv(u.T) @ np.diag(e) @ u.T,
#                               P.toarray(), atol=1e-10)
#    np.testing.assert_allclose(np.abs(e[0]), 1)
#    stationary = np.abs(u.T[0])

    e, u = sparse.linalg.eigs(P.T, k=1, which='LR')
    np.testing.assert_allclose(e, 1)
    stationary = np.abs(u).squeeze()
    assert np.all(stationary < 0.71)

    colorbar = False if type(graph) is pg.graphs.Ring else True
    graph.plot(stationary, colorbar=colorbar, ax=ax, title='$xP = x$')
    ax.set_axis_off()

fig.tight_layout()

Estimated memory usage: 9 MB