Graphs¶
The pygsp.graphs module implements the graph class hierarchy. A graph
object is either constructed from an adjacency matrix, or by instantiating one
of the built-in graph models.
Interface¶
The Graph base class allows to construct a graph object from any
adjacency matrix and provides a common interface to that object. Derived
classes then allows to instantiate various standard graph models.
Matrix operators¶
Graph.W |
|
Graph.L |
|
Graph.U |
Fourier basis (eigenvectors of the Laplacian). |
Graph.D |
Differential operator (for gradient and divergence). |
Checks¶
Graph.check_weights() |
Check the characteristics of the weights matrix. |
Graph.is_connected([recompute]) |
Check the strong connectivity of the graph (cached). |
Graph.is_directed([recompute]) |
Check if the graph has directed edges (cached). |
Attributes computation¶
Graph.compute_laplacian([lap_type]) |
Compute a graph Laplacian. |
Graph.estimate_lmax([recompute]) |
Estimate the Laplacian’s largest eigenvalue (cached). |
Graph.compute_fourier_basis([recompute]) |
Compute the Fourier basis of the graph (cached). |
Graph.compute_differential_operator() |
Compute the graph differential operator (cached). |
Differential operators¶
Graph.grad(s) |
Compute the gradient of a graph signal. |
Graph.div(s) |
Compute the divergence of a graph signal. |
Localization¶
Graph.modulate(f, k) |
Modulate the signal f to the frequency k. |
Graph.translate(f, i) |
Translate the signal f to the node i. |
Transforms (frequency and vertex-frequency)¶
Graph.gft(s) |
Compute the graph Fourier transform. |
Graph.igft(s_hat) |
Compute the inverse graph Fourier transform. |
Graph.gft_windowed(g, f[, lowmemory]) |
Windowed graph Fourier transform. |
Graph.gft_windowed_gabor(s, k) |
Gabor windowed graph Fourier transform. |
Graph.gft_windowed_normalized(g, f[, lowmemory]) |
Normalized windowed graph Fourier transform. |
Plotting¶
Graph.plot(**kwargs) |
Plot the graph. |
Graph.plot_signal(signal, **kwargs) |
Plot a signal on that graph. |
Graph.plot_spectrogram(**kwargs) |
Plot the graph’s spectrogram. |
Others¶
Graph.get_edge_list() |
Return an edge list, an alternative representation of the graph. |
Graph.set_coordinates([kind]) |
Set node’s coordinates (their position when plotting). |
Graph.subgraph(ind) |
Create a subgraph given indices. |
Graph.extract_components() |
Split the graph into connected components. |
Graph models¶
Airfoil(**kwargs) |
Airfoil graph. |
BarabasiAlbert([N, m0, m, seed]) |
Barabasi-Albert preferential attachment. |
Comet([N, k]) |
Comet graph. |
Community([N, Nc, min_comm, min_deg, …]) |
Community graph. |
DavidSensorNet([N, seed]) |
Sensor network. |
ErdosRenyi([N, p, directed, self_loops, …]) |
Erdos Renyi graph. |
FullConnected([N]) |
Fully connected graph. |
Grid2d([N1, N2]) |
2-dimensional grid graph. |
Logo(**kwargs) |
GSP logo. |
LowStretchTree([k]) |
Low stretch tree. |
Minnesota([connect]) |
Minnesota road network (from MatlabBGL). |
Path([N]) |
Path graph. |
RandomRegular([N, k, maxIter, seed]) |
Random k-regular graph. |
RandomRing([N, seed]) |
Ring graph with randomly sampled nodes. |
Ring([N, k]) |
K-regular ring graph. |
Sensor([N, Nc, regular, n_try, distribute, …]) |
Random sensor graph. |
StochasticBlockModel([N, k, z, M, p, q, …]) |
Stochastic Block Model (SBM). |
SwissRoll([N, a, b, dim, thresh, s, noise, …]) |
Sampled Swiss roll manifold. |
Torus([Nv, Mv]) |
Sampled torus manifold. |
Nearest-neighbors graphs constructed from point clouds¶
NNGraph(Xin[, NNtype, use_flann, center, …]) |
Nearest-neighbor graph from given point cloud. |
Bunny(**kwargs) |
Stanford bunny (NN-graph). |
Cube([radius, nb_pts, nb_dim, sampling, seed]) |
Hyper-cube (NN-graph). |
ImgPatches(img[, patch_shape, n_nbrs, …]) |
NN-graph between patches of an image. |
Grid2dImgPatches(img[, patch_shape, n_nbrs, …]) |
Union of a patch graph with a 2D grid graph. |
Sphere([radius, nb_pts, nb_dim, sampling, seed]) |
Spherical-shaped graph (NN-graph). |
TwoMoons([moontype, dim, sigmag, N, sigmad, …]) |
Two Moons (NN-graph). |
-
class
pygsp.graphs.Graph(W, gtype='unknown', lap_type='combinatorial', coords=None, plotting={}, **kwargs)[source]¶ Base graph class.
- Provide a common interface (and implementation) to graph objects.
- Can be instantiated to construct custom graphs from a weight matrix.
- Initialize attributes for derived classes.
Parameters: W : sparse matrix or ndarray
The weight matrix which encodes the graph.
gtype : string
Graph type, a free-form string to help us recognize the kind of graph we are dealing with (default is ‘unknown’).
lap_type : ‘combinatorial’, ‘normalized’
The type of Laplacian to be computed by
compute_laplacian()(default is ‘combinatorial’).coords : ndarray
Vertices coordinates (default is None).
plotting : dict
Plotting parameters.
perform_checks : bool
Whether to check if the graph is connected. Warn if not.
Examples
>>> W = np.arange(4).reshape(2, 2) >>> G = graphs.Graph(W)
Attributes
N (int) the number of nodes / vertices in the graph. Ne (int) the number of edges / links in the graph, i.e. connections between nodes. W (sparse matrix or ndarray) the weight matrix which contains the weights of the connections. It is represented as an N-by-N matrix of floats. \(W_{i,j} = 0\) means that there is no direct connection from i to j. A (sparse matrix or ndarray) the adjacency matrix defines which edges exist on the graph. It is represented as an N-by-N matrix of booleans. \(A_{i,j}\) is True if \(W_{i,j} > 0\). d (ndarray) the degree vector is a vector of length N which represents the number of edges connected to each node. gtype (string) the graph type is a short description of the graph object designed to help sorting the graphs. L (sparse matrix or ndarray) the graph Laplacian, an N-by-N matrix computed from W. lap_type (‘normalized’, ‘combinatorial’) the kind of Laplacian that was computed by compute_laplacian().coords (ndarray) vertices coordinates in 2D or 3D space. Used for plotting only. Default is None. plotting (dict) plotting parameters. -
check_weights()[source]¶ Check the characteristics of the weights matrix.
Returns: A dict of bools containing informations about the matrix
has_inf_val : bool
True if the matrix has infinite values else false
has_nan_value : bool
True if the matrix has a “not a number” value else false
is_not_square : bool
True if the matrix is not square else false
diag_is_not_zero : bool
True if the matrix diagonal has not only zeros else false
Examples
>>> W = np.arange(4).reshape(2, 2) >>> G = graphs.Graph(W) >>> cw = G.check_weights() >>> cw == {'has_inf_val': False, 'has_nan_value': False, ... 'is_not_square': False, 'diag_is_not_zero': True} True
-
compute_differential_operator()¶ Compute the graph differential operator (cached).
The differential operator is a matrix such that
\[L = D^T D,\]where \(D\) is the differential operator and \(L\) is the graph Laplacian. It is used to compute the gradient and the divergence of a graph signal, see
grad()anddiv().The result is cached and accessible by the
Dproperty.Examples
>>> G = graphs.Logo() >>> G.N, G.Ne (1130, 3131) >>> G.compute_differential_operator() >>> G.D.shape == (G.Ne, G.N) True
-
compute_fourier_basis(recompute=False)¶ Compute the Fourier basis of the graph (cached).
The result is cached and accessible by the
U,e,lmax, andmuproperties.Parameters: recompute: bool
Force to recompute the Fourier basis if already existing.
Notes
‘G.compute_fourier_basis()’ computes a full eigendecomposition of the graph Laplacian \(L\) such that:
\[L = U \Lambda U^*,\]where \(\Lambda\) is a diagonal matrix of eigenvalues and the columns of \(U\) are the eigenvectors.
G.e is a vector of length G.N containing the Laplacian eigenvalues. The largest eigenvalue is stored in G.lmax. The eigenvectors are stored as column vectors of G.U in the same order that the eigenvalues. Finally, the coherence of the Fourier basis is found in G.mu.
References
See [Chu97].
Examples
>>> G = graphs.Torus() >>> G.compute_fourier_basis() >>> G.U.shape (256, 256) >>> G.e.shape (256,) >>> G.lmax == G.e[-1] True >>> G.mu < 1 True
-
compute_laplacian(lap_type='combinatorial')[source]¶ Compute a graph Laplacian.
The result is accessible by the L attribute.
Parameters: lap_type : ‘combinatorial’, ‘normalized’
The type of Laplacian to compute. Default is combinatorial.
Notes
For undirected graphs, the combinatorial Laplacian is defined as
\[L = D - W,\]where \(W\) is the weight matrix and \(D\) the degree matrix, and the normalized Laplacian is defined as
\[L = I - D^{-1/2} W D^{-1/2},\]where \(I\) is the identity matrix.
Examples
>>> G = graphs.Sensor(50) >>> G.L.shape (50, 50) >>> >>> G.compute_laplacian('combinatorial') >>> G.compute_fourier_basis() >>> -1e-10 < G.e[0] < 1e-10 # Smallest eigenvalue close to 0. True >>> >>> G.compute_laplacian('normalized') >>> G.compute_fourier_basis(recompute=True) >>> -1e-10 < G.e[0] < 1e-10 < G.e[-1] < 2 # Spectrum in [0, 2]. True
-
copy_graph_attributes(Gn, ctype=True)[source]¶ Copy some parameters of the graph into a given one.
Parameters: G : Graph structure
ctype : bool
Flag to select what to copy (Default is True)
Gn : Graph structure
The graph where the parameters will be copied
Returns: Gn : Partial graph structure
Examples
>>> Torus = graphs.Torus() >>> G = graphs.TwoMoons() >>> G.copy_graph_attributes(ctype=False, Gn=Torus);
-
div(s)¶ Compute the divergence of a graph signal.
The divergence of a signal \(s\) is defined as
\[y = D^T s,\]where \(D\) is the differential operator
D.Parameters: s : ndarray
Signal of length G.Ne/2 living on the edges (non-directed graph).
Returns: s_div : ndarray
Divergence signal of length G.N living on the nodes.
Examples
>>> G = graphs.Logo() >>> G.N, G.Ne (1130, 3131) >>> s = np.random.normal(size=G.Ne) >>> s_div = G.div(s) >>> s_grad = G.grad(s_div)
-
estimate_lmax(recompute=False)[source]¶ Estimate the Laplacian’s largest eigenvalue (cached).
The result is cached and accessible by the
lmaxproperty.Exact value given by the eigendecomposition of the Laplacian, see
compute_fourier_basis(). That estimation is much faster than the eigendecomposition.Parameters: recompute : boolean
Force to recompute the largest eigenvalue. Default is false.
Notes
Runs the implicitly restarted Lanczos method with a large tolerance, then increases the calculated largest eigenvalue by 1 percent. For much of the PyGSP machinery, we need to approximate wavelet kernels on an interval that contains the spectrum of L. The only cost of using a larger interval is that the polynomial approximation over the larger interval may be a slightly worse approximation on the actual spectrum. As this is a very mild effect, it is not necessary to obtain very tight bounds on the spectrum of L.
Examples
>>> G = graphs.Logo() >>> G.compute_fourier_basis() >>> print('{:.2f}'.format(G.lmax)) 13.78 >>> G = graphs.Logo() >>> G.estimate_lmax(recompute=True) >>> print('{:.2f}'.format(G.lmax)) 13.92
-
extract_components()[source]¶ Split the graph into connected components.
See
is_connected()for the method used to determine connectedness.Returns: graphs : list
A list of graph structures. Each having its own node list and weight matrix. If the graph is directed, add into the info parameter the information about the source nodes and the sink nodes.
Examples
>>> from scipy import sparse >>> W = sparse.rand(10, 10, 0.2) >>> W = utils.symmetrize(W) >>> G = graphs.Graph(W=W) >>> components = G.extract_components() >>> has_sinks = 'sink' in components[0].info >>> sinks_0 = components[0].info['sink'] if has_sinks else []
-
get_edge_list()[source]¶ Return an edge list, an alternative representation of the graph.
The weighted adjacency matrix is the canonical form used in this package to represent a graph as it is the easiest to work with when considering spectral methods.
Returns: v_in : vector of int
v_out : vector of int
weights : vector of float
Examples
>>> G = graphs.Logo() >>> v_in, v_out, weights = G.get_edge_list() >>> v_in.shape, v_out.shape, weights.shape ((3131,), (3131,), (3131,))
-
gft(s)¶ Compute the graph Fourier transform.
The graph Fourier transform of a signal \(s\) is defined as
\[\hat{s} = U^* s,\]where \(U\) is the Fourier basis attr:U and \(U^*\) denotes the conjugate transpose or Hermitian transpose of \(U\).
Parameters: s : ndarray
Graph signal in the vertex domain.
Returns: s_hat : ndarray
Representation of s in the Fourier domain.
Examples
>>> G = graphs.Logo() >>> G.compute_fourier_basis() >>> s = np.random.normal(size=(G.N, 5, 1)) >>> s_hat = G.gft(s) >>> s_star = G.igft(s_hat) >>> np.all((s - s_star) < 1e-10) True
-
gft_windowed(g, f, lowmemory=True)¶ Windowed graph Fourier transform.
Parameters: g : ndarray or Filter
Window (graph signal or kernel).
f : ndarray
Graph signal in the vertex domain.
lowmemory : bool
Use less memory (default=True).
Returns: C : ndarray
Coefficients.
-
gft_windowed_gabor(s, k)¶ Gabor windowed graph Fourier transform.
Parameters: s : ndarray
Graph signal in the vertex domain.
k : function
Gabor kernel. See
pygsp.filters.Gabor.Returns: s : ndarray
Vertex-frequency representation of the signals.
Examples
>>> G = graphs.Logo() >>> s = np.random.normal(size=(G.N, 2)) >>> s = G.gft_windowed_gabor(s, lambda x: x/(1.-x)) >>> s.shape (1130, 2, 1130)
-
gft_windowed_normalized(g, f, lowmemory=True)¶ Normalized windowed graph Fourier transform.
Parameters: g : ndarray
Window.
f : ndarray
Graph signal in the vertex domain.
lowmemory : bool
Use less memory. (default = True)
Returns: C : ndarray
Coefficients.
-
grad(s)¶ Compute the gradient of a graph signal.
The gradient of a signal \(s\) is defined as
\[y = D s,\]where \(D\) is the differential operator
D.Parameters: s : ndarray
Signal of length G.N living on the nodes.
Returns: s_grad : ndarray
Gradient signal of length G.Ne/2 living on the edges (non-directed graph).
Examples
>>> G = graphs.Logo() >>> G.N, G.Ne (1130, 3131) >>> s = np.random.normal(size=G.N) >>> s_grad = G.grad(s) >>> s_div = G.div(s_grad) >>> np.linalg.norm(s_div - G.L.dot(s)) < 1e-10 True
-
igft(s_hat)¶ Compute the inverse graph Fourier transform.
The inverse graph Fourier transform of a Fourier domain signal \(\hat{s}\) is defined as
\[s = U \hat{s},\]where \(U\) is the Fourier basis
U.Parameters: s_hat : ndarray
Graph signal in the Fourier domain.
Returns: s : ndarray
Representation of s_hat in the vertex domain.
Examples
>>> G = graphs.Logo() >>> G.compute_fourier_basis() >>> s_hat = np.random.normal(size=(G.N, 5, 1)) >>> s = G.igft(s_hat) >>> s_hat_star = G.gft(s) >>> np.all((s_hat - s_hat_star) < 1e-10) True
-
is_connected(recompute=False)[source]¶ Check the strong connectivity of the graph (cached).
It uses DFS travelling on graph to ensure that each node is visited. For undirected graphs, starting at any vertex and trying to access all others is enough. For directed graphs, one needs to check that a random vertex is accessible by all others and can access all others. Thus, we can transpose the adjacency matrix and compute again with the same starting point in both phases.
Parameters: recompute: bool
Force to recompute the connectivity if already known.
Returns: connected : bool
True if the graph is connected.
Examples
>>> from scipy import sparse >>> W = sparse.rand(10, 10, 0.2) >>> G = graphs.Graph(W=W) >>> connected = G.is_connected()
-
is_directed(recompute=False)[source]¶ Check if the graph has directed edges (cached).
In this framework, we consider that a graph is directed if and only if its weight matrix is non symmetric.
Parameters: recompute : bool
Force to recompute the directedness if already known.
Returns: directed : bool
True if the graph is directed.
Notes
Can also be used to check if a matrix is symmetrical
Examples
>>> from scipy import sparse >>> W = sparse.rand(10, 10, 0.2) >>> G = graphs.Graph(W=W) >>> directed = G.is_directed()
-
modulate(f, k)[source]¶ Modulate the signal f to the frequency k.
Parameters: f : ndarray
Signal (column)
k : int
Index of frequencies
Returns: fm : ndarray
Modulated signal
-
set_coordinates(kind='spring', **kwargs)[source]¶ Set node’s coordinates (their position when plotting).
Parameters: kind : string or array-like
Kind of coordinates to generate. It controls the position of the nodes when plotting the graph. Can either pass an array of size Nx2 or Nx3 to set the coordinates manually or the name of a layout algorithm. Available algorithms: community2D, random2D, random3D, ring2D, line1D, spring. Default is ‘spring’.
kwargs : dict
Additional parameters to be passed to the Fruchterman-Reingold force-directed algorithm when kind is spring.
Examples
>>> G = graphs.ErdosRenyi() >>> G.set_coordinates() >>> G.plot()
-
subgraph(ind)[source]¶ Create a subgraph given indices.
Parameters: ind : list
Nodes to keep
Returns: sub_G : Graph
Subgraph
Examples
>>> W = np.arange(16).reshape(4, 4) >>> G = graphs.Graph(W) >>> ind = [1, 3] >>> sub_G = G.subgraph(ind)
-
translate(f, i)¶ Translate the signal f to the node i.
Parameters: f : ndarray
Signal
i : int
Indices of vertex
Returns: ft : translate signal
-
update_graph_attr(*args, **kwargs)[source]¶ Recompute some attribute of the graph.
Parameters: args: list of string
the arguments that will be not changed and not re-compute.
kwargs: Dictionnary
The arguments with their new value.
Returns: The same Graph with some updated values.
Notes
This method is useful if you want to give a new weight matrix (W) and compute the adjacency matrix (A) and more again. The valid attributes are [‘W’, ‘A’, ‘N’, ‘d’, ‘Ne’, ‘gtype’, ‘directed’, ‘coords’, ‘lap_type’, ‘L’, ‘plotting’]
Examples
>>> G = graphs.Ring(N=10) >>> newW = G.W >>> newW[1] = 1 >>> G.update_graph_attr('N', 'd', W=newW)
Updates all attributes of G except ‘N’ and ‘d’
-
D¶ Differential operator (for gradient and divergence).
Is computed by
compute_differential_operator().
-
U¶ Fourier basis (eigenvectors of the Laplacian).
Is computed by
compute_fourier_basis().
-
e¶ Eigenvalues of the Laplacian (square of graph frequencies).
Is computed by
compute_fourier_basis().
-
lmax¶ Largest eigenvalue of the graph Laplacian.
Can be exactly computed by
compute_fourier_basis()or approximated byestimate_lmax().
-
mu¶ Coherence of the Fourier basis.
Is computed by
compute_fourier_basis().
-
class
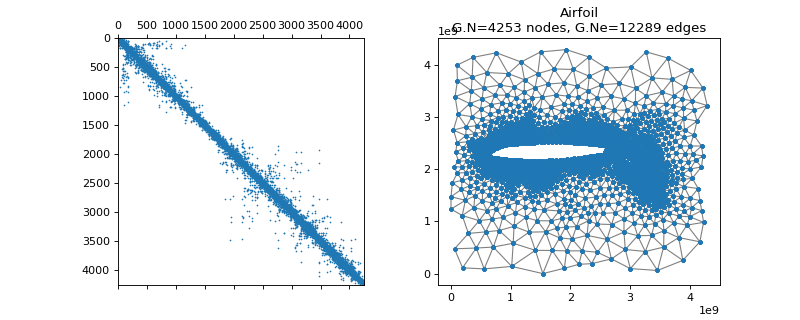
pygsp.graphs.Airfoil(**kwargs)[source]¶ Airfoil graph.
Examples
>>> import matplotlib.pyplot as plt >>> G = graphs.Airfoil() >>> fig, axes = plt.subplots(1, 2) >>> _ = axes[0].spy(G.W, markersize=0.5) >>> G.plot(show_edges=True, ax=axes[1])
-
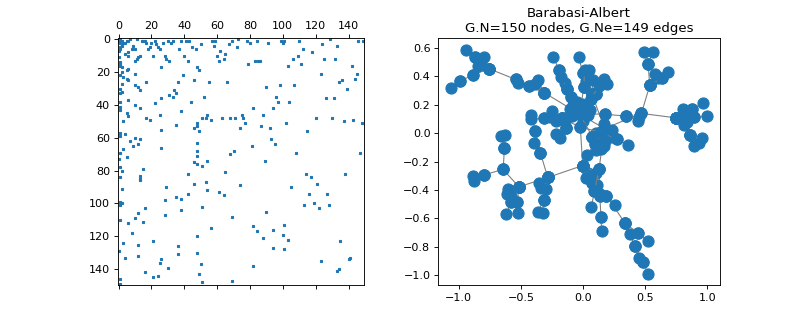
class
pygsp.graphs.BarabasiAlbert(N=1000, m0=1, m=1, seed=None, **kwargs)[source]¶ Barabasi-Albert preferential attachment.
The Barabasi-Albert graph is constructed by connecting nodes in two steps. First, m0 nodes are created. Then, nodes are added one by one.
By lack of clarity, we take the liberty to create it as follows:
- the m0 initial nodes are disconnected,
- each node is connected to m of the older nodes with a probability distribution depending of the node-degrees of the other nodes, \(p_n(i) = \frac{1 + k_i}{\sum_j{1 + k_j}}\).
Parameters: N : int
Number of nodes (default is 1000)
m0 : int
Number of initial nodes (default is 1)
m : int
Number of connections at each step (default is 1) m can never be larger than m0.
seed : int
Seed for the random number generator (for reproducible graphs).
Examples
>>> import matplotlib.pyplot as plt >>> G = graphs.BarabasiAlbert(N=150, seed=42) >>> G.set_coordinates(kind='spring', seed=42) >>> fig, axes = plt.subplots(1, 2) >>> _ = axes[0].spy(G.W, markersize=2) >>> G.plot(ax=axes[1])
-
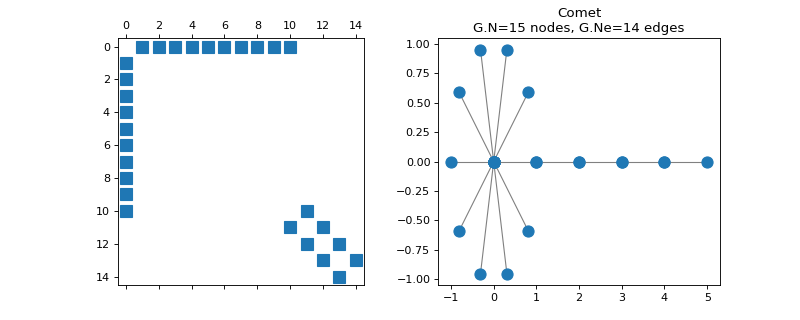
class
pygsp.graphs.Comet(N=32, k=12, **kwargs)[source]¶ Comet graph.
The comet graph is a path graph with a star of degree k at its end.
Parameters: N : int
Number of nodes.
k : int
Degree of center vertex.
Examples
>>> import matplotlib.pyplot as plt >>> G = graphs.Comet(15, 10) >>> fig, axes = plt.subplots(1, 2) >>> _ = axes[0].spy(G.W) >>> G.plot(ax=axes[1])
-
class
pygsp.graphs.Community(N=256, Nc=None, min_comm=None, min_deg=0, comm_sizes=None, size_ratio=1, world_density=None, comm_density=None, k_neigh=None, epsilon=None, seed=None, **kwargs)[source]¶ Community graph.
Parameters: N : int
Number of nodes (default = 256).
Nc : int (optional)
Number of communities (default = \(\lfloor \sqrt{N}/2 \rceil\)).
min_comm : int (optional)
Minimum size of the communities (default = \(\lfloor N/Nc/3 \rceil\)).
min_deg : int (optional)
NOT IMPLEMENTED. Minimum degree of each node (default = 0).
comm_sizes : int (optional)
Size of the communities (default = random).
size_ratio : float (optional)
Ratio between the radius of world and the radius of communities (default = 1).
world_density : float (optional)
Probability of a random edge between two different communities (default = 1/N).
comm_density : float (optional)
Probability of a random edge inside any community (default = None, which implies k_neigh or epsilon will be used to determine intra-edges).
k_neigh : int (optional)
Number of intra-community connections. Not used if comm_density is defined (default = None, which implies comm_density or epsilon will be used to determine intra-edges).
epsilon : float (optional)
Largest distance at which two nodes sharing a community are connected. Not used if k_neigh or comm_density is defined (default = \(\sqrt{2\sqrt{N}}/2\)).
seed : int
Seed for the random number generator (for reproducible graphs).
Examples
>>> import matplotlib.pyplot as plt >>> G = graphs.Community(N=250, Nc=3, comm_sizes=[50, 120, 80], seed=42) >>> fig, axes = plt.subplots(1, 2) >>> _ = axes[0].spy(G.W, markersize=0.5) >>> G.plot(ax=axes[1])
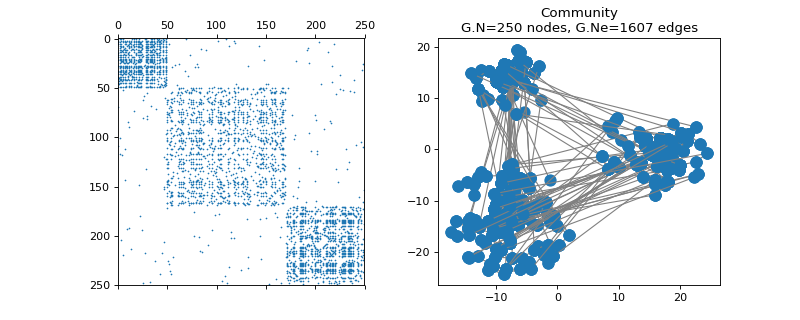
-
class
pygsp.graphs.DavidSensorNet(N=64, seed=None, **kwargs)[source]¶ Sensor network.
Parameters: N : int
Number of vertices (default = 64). Values of 64 and 500 yield pre-computed and saved graphs. Other values yield randomly generated graphs.
seed : int
Seed for the random number generator (for reproducible graphs).
Examples
>>> import matplotlib.pyplot as plt >>> G = graphs.DavidSensorNet() >>> fig, axes = plt.subplots(1, 2) >>> _ = axes[0].spy(G.W, markersize=2) >>> G.plot(ax=axes[1])
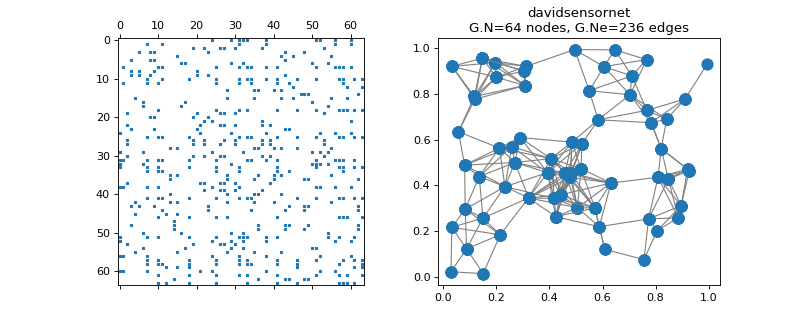
-
class
pygsp.graphs.ErdosRenyi(N=100, p=0.1, directed=False, self_loops=False, connected=False, max_iter=10, seed=None, **kwargs)[source]¶ Erdos Renyi graph.
The Erdos Renyi graph is constructed by randomly connecting nodes. Each edge is included in the graph with probability p, independently from any other edge. All edge weights are equal to 1.
Parameters: N : int
Number of nodes (default is 100).
p : float
Probability to connect a node with another one.
directed : bool
Allow directed edges if True (default is False).
self_loops : bool
Allow self loops if True (default is False).
connected : bool
Force the graph to be connected (default is False).
max_iter : int
Maximum number of trials to get a connected graph (default is 10).
seed : int
Seed for the random number generator (for reproducible graphs).
Examples
>>> import matplotlib.pyplot as plt >>> G = graphs.ErdosRenyi(N=64, seed=42) >>> G.set_coordinates(kind='spring', seed=42) >>> fig, axes = plt.subplots(1, 2) >>> _ = axes[0].spy(G.W, markersize=2) >>> G.plot(ax=axes[1])
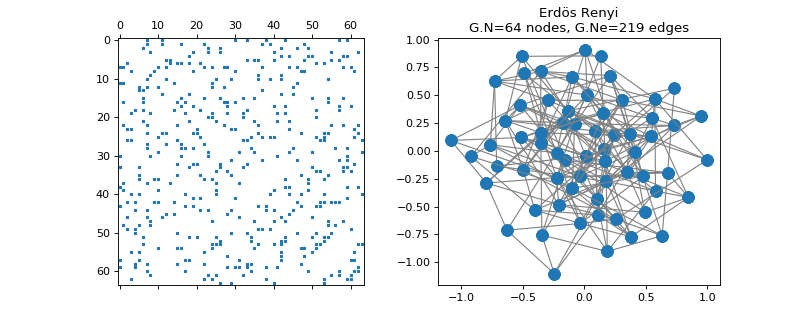
-
class
pygsp.graphs.FullConnected(N=10, **kwargs)[source]¶ Fully connected graph.
All weights are set to 1. There is no self-connections.
Parameters: N : int
Number of vertices (default = 10)
Examples
>>> import matplotlib.pyplot as plt >>> G = graphs.FullConnected(N=20) >>> G.set_coordinates(kind='spring', seed=42) >>> fig, axes = plt.subplots(1, 2) >>> _ = axes[0].spy(G.W, markersize=5) >>> G.plot(ax=axes[1])
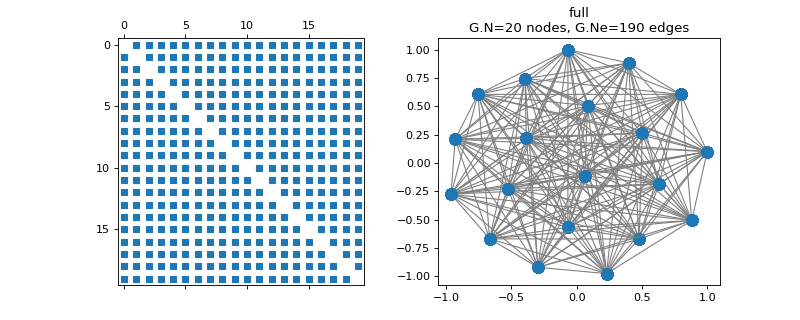
-
class
pygsp.graphs.Grid2d(N1=16, N2=None, **kwargs)[source]¶ 2-dimensional grid graph.
Parameters: N1 : int
Number of vertices along the first dimension.
N2 : int
Number of vertices along the second dimension (default N1).
Examples
>>> import matplotlib.pyplot as plt >>> G = graphs.Grid2d(N1=5, N2=4) >>> fig, axes = plt.subplots(1, 2) >>> _ = axes[0].spy(G.W) >>> G.plot(ax=axes[1])
-
class
pygsp.graphs.Logo(**kwargs)[source]¶ GSP logo.
Examples
>>> import matplotlib.pyplot as plt >>> G = graphs.Logo() >>> fig, axes = plt.subplots(1, 2) >>> _ = axes[0].spy(G.W, markersize=0.5) >>> G.plot(ax=axes[1])
-
class
pygsp.graphs.LowStretchTree(k=6, **kwargs)[source]¶ Low stretch tree.
Build the root of a low stretch tree on a grid of points. There are \(2k\) points on each side of the grid, and therefore \(2^{2k}\) vertices in total. The edge weights are all equal to 1.
Parameters: k : int
\(2^k\) points on each side of the grid of vertices.
Examples
>>> import matplotlib.pyplot as plt >>> G = graphs.LowStretchTree(k=2) >>> fig, axes = plt.subplots(1, 2) >>> _ = axes[0].spy(G.W) >>> G.plot(ax=axes[1])
-
class
pygsp.graphs.Minnesota(connect=True, **kwargs)[source]¶ Minnesota road network (from MatlabBGL).
Parameters: connect : bool
If True, the adjacency matrix is adjusted so that all edge weights are equal to 1, and the graph is connected. Set to False to get the original disconnected graph.
References
See [Gle].
Examples
>>> import matplotlib.pyplot as plt >>> G = graphs.Minnesota() >>> fig, axes = plt.subplots(1, 2) >>> _ = axes[0].spy(G.W, markersize=0.5) >>> G.plot(ax=axes[1])
-
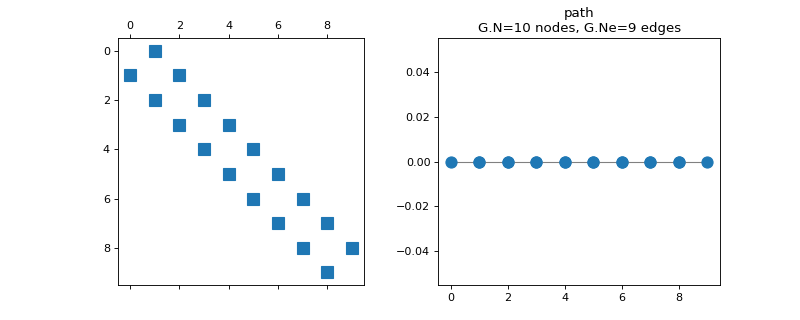
class
pygsp.graphs.Path(N=16, **kwargs)[source]¶ Path graph.
Parameters: N : int
Number of vertices.
References
See [Str99] for more informations.
Examples
>>> import matplotlib.pyplot as plt >>> G = graphs.Path(N=10) >>> fig, axes = plt.subplots(1, 2) >>> _ = axes[0].spy(G.W) >>> G.plot(ax=axes[1])
-
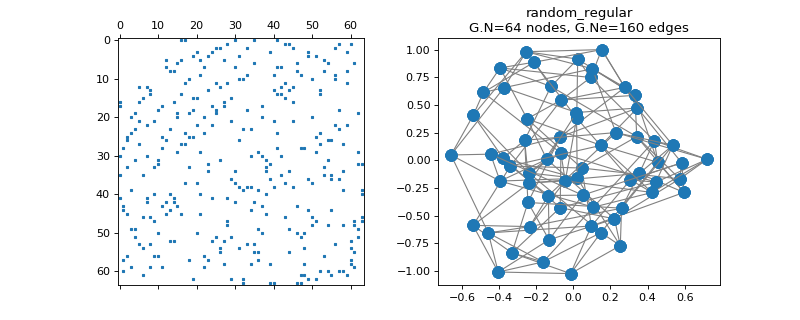
class
pygsp.graphs.RandomRegular(N=64, k=6, maxIter=10, seed=None, **kwargs)[source]¶ Random k-regular graph.
The random regular graph has the property that every node is connected to k other nodes. That graph is simple (without loops or double edges), k-regular (each vertex is adjacent to k nodes), and undirected.
Parameters: N : int
Number of nodes (default is 64)
k : int
Number of connections, or degree, of each node (default is 6)
maxIter : int
Maximum number of iterations (default is 10)
seed : int
Seed for the random number generator (for reproducible graphs).
Notes
The pairing model algorithm works as follows. First create n*d half edges. Then repeat as long as possible: pick a pair of half edges and if it’s legal (doesn’t create a loop nor a double edge) add it to the graph.
References
See [KV03]. This code has been adapted from matlab to python.
Examples
>>> import matplotlib.pyplot as plt >>> G = graphs.RandomRegular(N=64, k=5, seed=42) >>> G.set_coordinates(kind='spring', seed=42) >>> fig, axes = plt.subplots(1, 2) >>> _ = axes[0].spy(G.W, markersize=2) >>> G.plot(ax=axes[1])
-
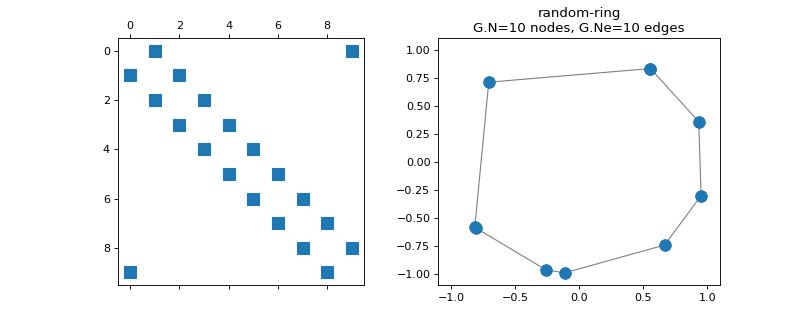
class
pygsp.graphs.RandomRing(N=64, seed=None, **kwargs)[source]¶ Ring graph with randomly sampled nodes.
Parameters: N : int
Number of vertices.
seed : int
Seed for the random number generator (for reproducible graphs).
Examples
>>> import matplotlib.pyplot as plt >>> G = graphs.RandomRing(N=10, seed=42) >>> fig, axes = plt.subplots(1, 2) >>> _ = axes[0].spy(G.W) >>> G.plot(ax=axes[1]) >>> _ = axes[1].set_xlim(-1.1, 1.1) >>> _ = axes[1].set_ylim(-1.1, 1.1)
-
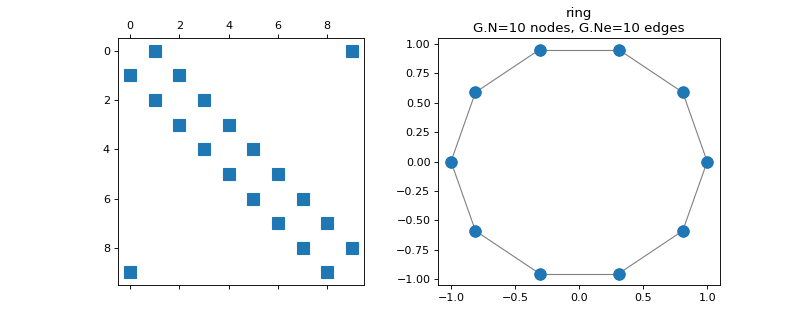
class
pygsp.graphs.Ring(N=64, k=1, **kwargs)[source]¶ K-regular ring graph.
Parameters: N : int
Number of vertices.
k : int
Number of neighbors in each direction.
Examples
>>> import matplotlib.pyplot as plt >>> G = graphs.Ring(N=10) >>> fig, axes = plt.subplots(1, 2) >>> _ = axes[0].spy(G.W) >>> G.plot(ax=axes[1])
-
class
pygsp.graphs.Sensor(N=64, Nc=2, regular=False, n_try=50, distribute=False, connected=True, seed=None, **kwargs)[source]¶ Random sensor graph.
Parameters: N : int
Number of nodes (default = 64)
Nc : int
Minimum number of connections (default = 2)
regular : bool
Flag to fix the number of connections to nc (default = False)
n_try : int
Number of attempt to create the graph (default = 50)
distribute : bool
To distribute the points more evenly (default = False)
connected : bool
To force the graph to be connected (default = True)
seed : int
Seed for the random number generator (for reproducible graphs).
Examples
>>> import matplotlib.pyplot as plt >>> G = graphs.Sensor(N=64, seed=42) >>> fig, axes = plt.subplots(1, 2) >>> _ = axes[0].spy(G.W, markersize=2) >>> G.plot(ax=axes[1])
-
class
pygsp.graphs.StochasticBlockModel(N=1024, k=5, z=None, M=None, p=0.7, q=None, directed=False, self_loops=False, connected=False, max_iter=10, seed=None, **kwargs)[source]¶ Stochastic Block Model (SBM).
The Stochastic Block Model graph is constructed by connecting nodes with a probability which depends on the cluster of the two nodes. One can define the clustering association of each node, denoted by vector z, but also the probability matrix M. All edge weights are equal to 1. By default, Mii > Mjk and nodes are uniformly clusterized.
Parameters: N : int
Number of nodes (default is 1024).
k : float
Number of classes (default is 5).
z : array_like
the vector of length N containing the association between nodes and classes (default is random uniform).
M : array_like
the k by k matrix containing the probability of connecting nodes based on their class belonging (default using p and q).
p : float or array_like
the diagonal value(s) for the matrix M. If scalar they all have the same value. Otherwise expect a length k vector (default is p = 0.7).
q : float or array_like
the off-diagonal value(s) for the matrix M. If scalar they all have the same value. Otherwise expect a k x k matrix, diagonal will be discarded (default is q = 0.3/k).
directed : bool
Allow directed edges if True (default is False).
self_loops : bool
Allow self loops if True (default is False).
connected : bool
Force the graph to be connected (default is False).
max_iter : int
Maximum number of trials to get a connected graph (default is 10).
seed : int
Seed for the random number generator (for reproducible graphs).
Examples
>>> import matplotlib.pyplot as plt >>> G = graphs.StochasticBlockModel( ... 100, k=3, p=[0.4, 0.6, 0.3], q=0.02, seed=42) >>> G.set_coordinates(kind='spring', seed=42) >>> fig, axes = plt.subplots(1, 2) >>> _ = axes[0].spy(G.W, markersize=0.8) >>> G.plot(ax=axes[1])
-
class
pygsp.graphs.SwissRoll(N=400, a=1, b=4, dim=3, thresh=1e-06, s=None, noise=False, srtype='uniform', seed=None, **kwargs)[source]¶ Sampled Swiss roll manifold.
Parameters: N : int
Number of vertices (default = 400)
a : int
(default = 1)
b : int
(default = 4)
dim : int
(default = 3)
thresh : float
(default = 1e-6)
s : float
sigma (default = sqrt(2./N))
noise : bool
Wether to add noise or not (default = False)
srtype : str
Swiss roll Type, possible arguments are ‘uniform’ or ‘classic’ (default = ‘uniform’)
seed : int
Seed for the random number generator (for reproducible graphs).
Examples
>>> import matplotlib.pyplot as plt >>> G = graphs.SwissRoll(N=200, seed=42) >>> fig = plt.figure() >>> ax1 = fig.add_subplot(121) >>> ax2 = fig.add_subplot(122, projection='3d') >>> _ = ax1.spy(G.W, markersize=1) >>> G.plot(ax=ax2)
-
class
pygsp.graphs.Torus(Nv=16, Mv=None, **kwargs)[source]¶ Sampled torus manifold.
Parameters: Nv : int
Number of vertices along the first dimension (default is 16)
Mv : int
Number of vertices along the second dimension (default is Nv)
References
See [Str99] for more informations.
Examples
>>> import matplotlib.pyplot as plt >>> G = graphs.Torus(10) >>> fig = plt.figure() >>> ax1 = fig.add_subplot(121) >>> ax2 = fig.add_subplot(122, projection='3d') >>> _ = ax1.spy(G.W, markersize=1.5) >>> G.plot(ax=ax2) >>> _ = ax2.set_zlim(-1.5, 1.5)
-
class
pygsp.graphs.NNGraph(Xin, NNtype='knn', use_flann=False, center=True, rescale=True, k=10, sigma=0.1, epsilon=0.01, gtype=None, plotting={}, symmetrize_type='average', dist_type='euclidean', order=0, **kwargs)[source]¶ Nearest-neighbor graph from given point cloud.
Parameters: Xin : ndarray
Input points, Should be an N-by-d matrix, where N is the number of nodes in the graph and d is the dimension of the feature space.
NNtype : string, optional
Type of nearest neighbor graph to create. The options are ‘knn’ for k-Nearest Neighbors or ‘radius’ for epsilon-Nearest Neighbors (default is ‘knn’).
use_flann : bool, optional
Use Fast Library for Approximate Nearest Neighbors (FLANN) or not. (default is False)
center : bool, optional
Center the data so that it has zero mean (default is True)
rescale : bool, optional
Rescale the data so that it lies in a l2-sphere (default is True)
k : int, optional
Number of neighbors for knn (default is 10)
sigma : float, optional
Width parameter of the similarity kernel (default is 0.1)
epsilon : float, optional
Radius for the epsilon-neighborhood search (default is 0.01)
gtype : string, optional
The type of graph (default is ‘nearest neighbors’)
plotting : dict, optional
Dictionary of plotting parameters. See
pygsp.plotting. (default is {})symmetrize_type : string, optional
Type of symmetrization to use for the adjacency matrix. See
pygsp.utils.symmetrization()for the options. (default is ‘average’)dist_type : string, optional
Type of distance to compute. See
pyflann.index.set_distance_type()for possible options. (default is ‘euclidean’)order : float, optional
Only used if dist_type is ‘minkowski’; represents the order of the Minkowski distance. (default is 0)
Examples
>>> import matplotlib.pyplot as plt >>> X = np.random.RandomState(42).uniform(size=(30, 2)) >>> G = graphs.NNGraph(X) >>> fig, axes = plt.subplots(1, 2) >>> _ = axes[0].spy(G.W, markersize=5) >>> G.plot(ax=axes[1])
-
class
pygsp.graphs.Bunny(**kwargs)[source]¶ Stanford bunny (NN-graph).
References
See [TL94].
Examples
>>> import matplotlib.pyplot as plt >>> G = graphs.Bunny() >>> fig = plt.figure() >>> ax1 = fig.add_subplot(121) >>> ax2 = fig.add_subplot(122, projection='3d') >>> _ = ax1.spy(G.W, markersize=0.1) >>> G.plot(ax=ax2)
-
class
pygsp.graphs.Cube(radius=1, nb_pts=300, nb_dim=3, sampling='random', seed=None, **kwargs)[source]¶ Hyper-cube (NN-graph).
Parameters: radius : float
Edge lenght (default = 1)
nb_pts : int
Number of vertices (default = 300)
nb_dim : int
Dimension (default = 3)
sampling : string
Variance of the distance kernel (default = ‘random’) (Can now only be ‘random’)
seed : int
Seed for the random number generator (for reproducible graphs).
Examples
>>> import matplotlib.pyplot as plt >>> G = graphs.Cube(seed=42) >>> fig = plt.figure() >>> ax1 = fig.add_subplot(121) >>> ax2 = fig.add_subplot(122, projection='3d') >>> _ = ax1.spy(G.W, markersize=0.5) >>> G.plot(ax=ax2)
-
class
pygsp.graphs.ImgPatches(img, patch_shape=(3, 3), n_nbrs=8, use_flann=True, dist_type='euclidean', symmetrize_type='fill', **kwargs)[source]¶ NN-graph between patches of an image.
Parameters: img : array
Input image.
patch_shape : tuple, optional
Dimensions of the patch window. Syntax: (height, width), or (height,), in which case width = height.
n_nbrs : int, optional
Number of neighbors to consider
dist_type : string, optional
Type of distance between patches to compute. See
pyflann.index.set_distance_type()for possible options.Examples
>>> import matplotlib.pyplot as plt >>> from skimage import data, img_as_float >>> img = img_as_float(data.camera()[::64, ::64]) >>> G = graphs.ImgPatches(img, use_flann=False) >>> G.set_coordinates(kind='spring', seed=42) >>> fig, axes = plt.subplots(1, 2) >>> _ = axes[0].spy(G.W, markersize=2) >>> G.plot(ax=axes[1])
-
class
pygsp.graphs.Grid2dImgPatches(img, patch_shape=(3, 3), n_nbrs=8, aggregate=<function Grid2dImgPatches.<lambda>>, **kwargs)[source]¶ Union of a patch graph with a 2D grid graph.
Parameters: img : array
Input image.
patch_shape : tuple, optional
Dimensions of the patch window. Syntax : (height, width).
n_nbrs : int
Number of neighbors to consider
dist_type : string
Type of distance between patches to compute. See
pyflann.index.set_distance_type()for possible options.aggregate: callable, optional
Function used for aggregating the weights Wp of the patch graph and the weigths Wg 2d grid graph. Default is
lambda Wp, Wg: Wp + Wg().Examples
>>> import matplotlib.pyplot as plt >>> from skimage import data, img_as_float >>> img = img_as_float(data.camera()[::64, ::64]) >>> G = graphs.Grid2dImgPatches(img, use_flann=False) >>> fig, axes = plt.subplots(1, 2) >>> _ = axes[0].spy(G.W, markersize=2) >>> G.plot(ax=axes[1])
-
class
pygsp.graphs.Sphere(radius=1, nb_pts=300, nb_dim=3, sampling='random', seed=None, **kwargs)[source]¶ Spherical-shaped graph (NN-graph).
Parameters: radius : flaot
Radius of the sphere (default = 1)
nb_pts : int
Number of vertices (default = 300)
nb_dim : int
Dimension (default = 3)
sampling : sting
Variance of the distance kernel (default = ‘random’) (Can now only be ‘random’)
seed : int
Seed for the random number generator (for reproducible graphs).
Examples
>>> import matplotlib.pyplot as plt >>> G = graphs.Sphere(nb_pts=100, seed=42) >>> fig = plt.figure() >>> ax1 = fig.add_subplot(121) >>> ax2 = fig.add_subplot(122, projection='3d') >>> _ = ax1.spy(G.W, markersize=1.5) >>> G.plot(ax=ax2)
-
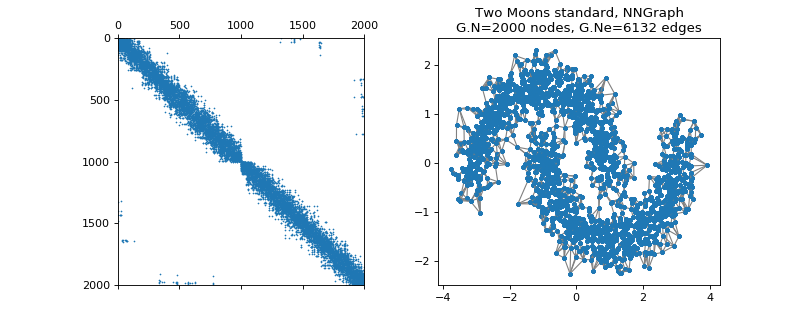
class
pygsp.graphs.TwoMoons(moontype='standard', dim=2, sigmag=0.05, N=400, sigmad=0.07, d=0.5, seed=None, **kwargs)[source]¶ Two Moons (NN-graph).
Parameters: moontype : ‘standard’ or ‘synthesized’
You have the freedom to chose if you want to create a standard two_moons graph or a synthesized one (default is ‘standard’). ‘standard’ : Create a two_moons graph from a based graph. ‘synthesized’ : Create a synthesized two_moon
sigmag : float
Variance of the distance kernel (default = 0.05)
dim : int
The dimensionality of the points (default = 2). Only valid for moontype == ‘standard’.
N : int
Number of vertices (default = 2000) Only valid for moontype == ‘synthesized’.
sigmad : float
Variance of the data (do not set it too high or you won’t see anything) (default = 0.05) Only valid for moontype == ‘synthesized’.
d : float
Distance of the two moons (default = 0.5) Only valid for moontype == ‘synthesized’.
seed : int
Seed for the random number generator (for reproducible graphs).
Examples
>>> import matplotlib.pyplot as plt >>> G = graphs.TwoMoons() >>> fig, axes = plt.subplots(1, 2) >>> _ = axes[0].spy(G.W, markersize=0.5) >>> G.plot(show_edges=True, ax=axes[1])